Why the proof of closure under addition in Linear Map is $(T+S)(u+v)$ instead of $(T+S)(u)$ and $(T)(u+v)$? - Mathematics Stack Exchange

I am reading Linear Algebra Done Right and want to prove that $L(V, W)$ is a vector space. I have read the solution here: Why the proof of closure under addition in Linear Map is $(T+S)(u+v)$ inst

Mathematics, Free Full-Text

Convolution - Wikipedia

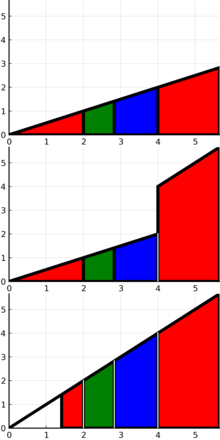
Geometric series - Wikipedia

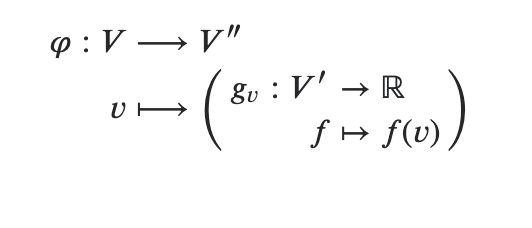
Double Dual Space: An Exercise in Abstraction, by Sam Boshar

Solved Problems For Problems 1-14, determine whether the

T:V ightarrow W$ be a linear map and $v_1v_n$ be basis for $V

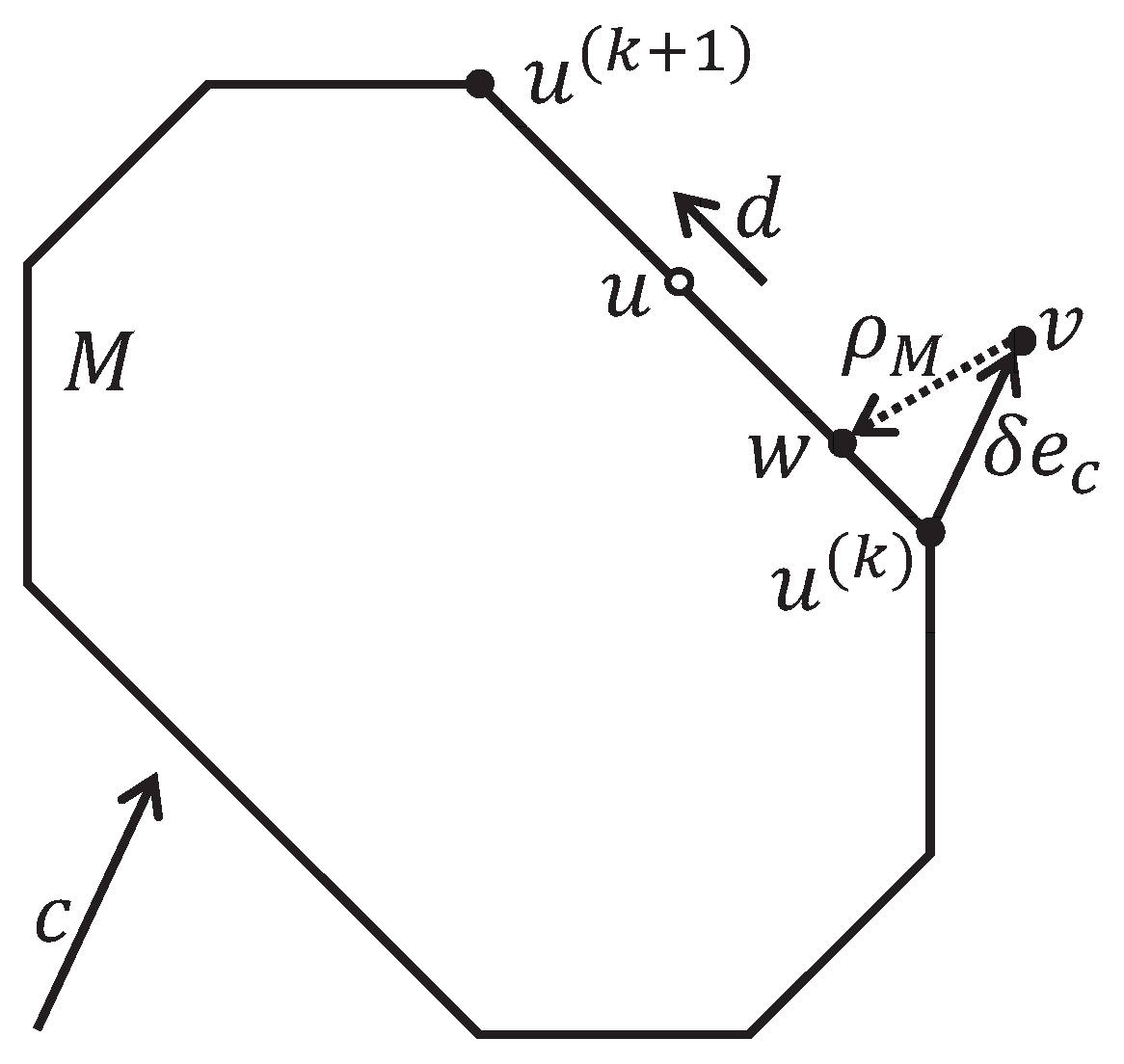
115 For a p V n system construct Legendre

Proving a function is a linear map - Mathematics Stack Exchange

How to Prove a Set is Not Closed Under Vector Addition